Tangent Circles Investigation

By

Cassian Mosha

Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

Given two circles that are tangent to each other then they have a common point. Now let’s consider two circles as shown below.

Figure 1

We will try to construct circle C that is tangent to both circles A and B. To do as such we need to pick two points one on each circle. The point on circle A will be an arbitrary point that we will use to construct a line through center A. Also the arbitrary point on circle B will connect to the center of circle B and will form a radius that we will use construct our tangent circle to both circles.

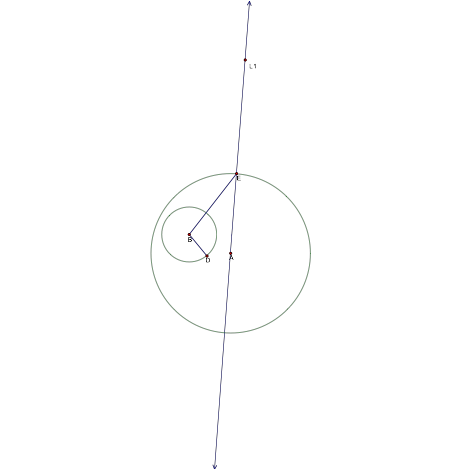
Figure 2

Then we will connect points E and D to form a triangle BDE. Then we will find the mid point of segment BE and construct a perpendicular line through this point. The intersection point on the perpendicular line L2 through line segment BE and line L1 is the locus point of the two given circles A and B. This locus point will be the center of the circle that is tangent to both circles.

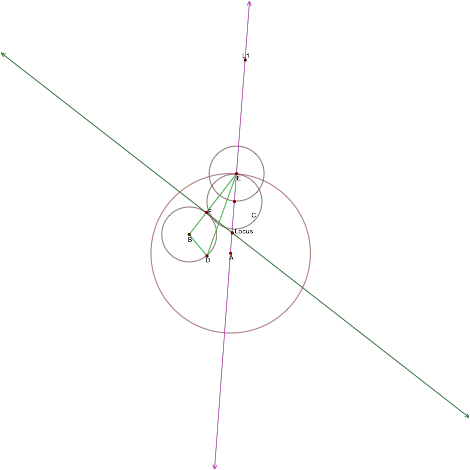
Figure 3

As we can see circle C is tangent to both circles A and B and if we animate point E we can describe some different features that the circles are showing while revolving at its tangential points.

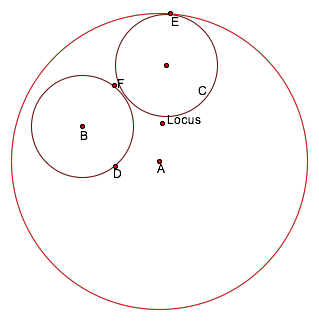
Figure 4

Figure 4 shows the tangential circle to both circles A and B and they are equidistant from the locus. No matter where the circles are the distance between the centers of circle A and B will always beequidistant from the locus. The locus is in line with the centers of the circles A and B since any line tangent to a circle is by definition perpendicular to the radius or diameter of the circle. The locus point when animated makes a small circle that is tangent to circle B and then makes another big circle that is partly overlapping with circle B and tangent to center A.

After constructing the tangent circle lets explore how to construct two circles tangent to a given circle at point P on the circle if we are given a line and a circle with center K.

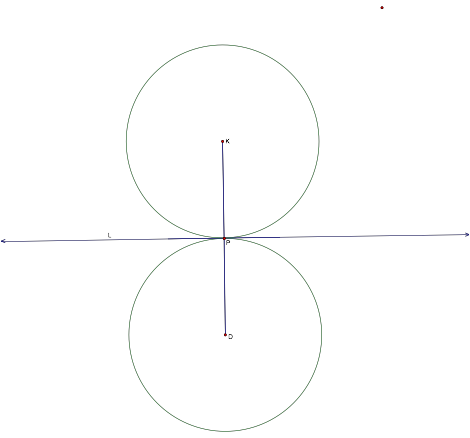
Figure 5

Using the tangent circle we constructed earlier, and using the observation of the animation and the fact that a tangent line is perpendicular to a radius, I constructed the circle first, then I chose a point on the circle construct a perpendicular to form the line. Then with the given line I took a segment of radius R and draw two circles using each end point as a center. The two circles gave me two new points, which I used to construct the circles that are tangent to each other, and tangent to the given line. The circles and the line intersect at point P as shown on figure 5.

Return